古代ギリシャの数学者が重視した「初等作図問題」は、一見すると変な制約が付いているように見えます。定規とコンパスを「自由に」使ってよければ、初等作図では不可能な角の 3 等分などの操作が実行できます。現代の代数学の観点から見れば、初等作図には美しい意味がありますが、それを知っていたはずもない紀元前の数学者が初等作図にこだわったことは、いにしえの数学者の鋭敏なセンスを物語っているような気がして、畏敬の念を抱かずにはいられません。
正 5 角形が定規とコンパスを使って描けることは、紀元前 300 年頃に成立したユークリッドの『原論』に既に記されているそうです。このように、許される操作だけを使って条件を満たす図形を描く方法を見つける問題を作図問題といい、中でも初等作図―いわゆる「定規とコンパスを使った作図」―の問題が古代ギリシャ文明の数学者によって盛んに研究されたのはよく知られているところです。
古代ギリシャの数学者は、次の三つの問題に対する初等作図の方法を見つけることができませんでした。これらは「三大作図問題」と呼ばれることになります。
これらの問題が初等作図可能でないことは、問題が提案された後 2000 年以上たった 19 世紀になって、代数学の道具を応用して証明されました。 19 世紀は、 5 次方程式の解の公式が存在しないことの証明 (Abel 1826) が得られ、それを基礎付けるガロア (Galois) 理論が成立した重要な時代です。角の 3 等分問題と立方倍積問題が初等作図不可能であることは 1836 年に Wantzel によって証明され、円積問題が初等作図不可能であることは円周率が超越数であること (Lindemann 1882) から導かれました。
でも、ちょっと待ってください。普通、定規には目盛りが付いています。角の 3 等分は、次のようにしたら定規とコンパスだけでできますよね? (アルキメデスの作図) (図の SVG ファイル)

あれれ、そうすると、角の 3 等分が初等作図できないというのと矛盾するのではありませんか?
初等作図で使う定規には、目盛りはありません。だから、上の手順 4 は実行できません。
では、初等作図で本当にできる操作とはいったい何でしょうか。それは、次の操作です。
これらの操作を有限回繰り返すことで条件を満たす図形を描く問題が、初等作図問題です。
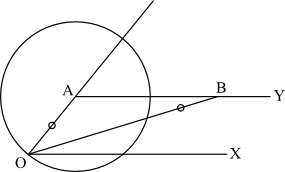
ここで次の初等作図問題を考えましょう。円とその外部にある点が与えられるので、与えられた点を通る円の接線を引いてください。もちろん、初等的にです。
「点を支点として定規を回転させながら、円に接する直線を探す」という操作では、初等作図可能であることを示したことになりません。そのような操作は上のリストに含まれていないからです。
次のようにすれば接線を引くことができます。与えられた点を A とします。 (図の SVG ファイル)
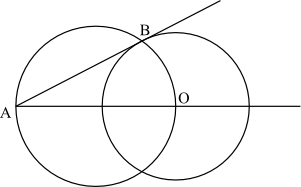
初等作図は意外と手間がかかりますね……。でも、定規を回転させるという動作を考えなくても円の接線が引けるというのは、なかなか面白いと思います。
こう考えてみると、初等作図というのはなんだか不思議な制約が付いているように見えます。どうして定規を回転しながら条件に合う直線を求めたり、定規の目盛りを使ったりしてはいけないのでしょう。そういう操作を許さない方が問題として面白いと考える数学者が、古代ギリシャからいたことは間違いありません。しかし、なぜ?
ギリシャ文明の数学では、ある図形が初等作図不可能であることを示すための道具はありませんでした。今では、どのような図形が初等作図可能で、どのような図形が初等作図不可能か、代数学を使って美しく特徴付けられています。同様の特徴付けは、初等作図を逸脱する一部の作図法についても知られています。しかし、初等作図のときの結果がすべての基礎にあることは間違いありません。ギリシャ文明の時代よりずっと発展した現代数学の観点から考えれば、初等作図というのはきわめて自然な制約なのです。
でも、ギリシャ文明の数学者がそのことを知っていたはずはありません。初等作図の代数的な特徴付けが美しいといっても、その特徴付けは 19 世紀になってようやく得られたのですから。なぜ彼らが初等作図にこだわったのか、僕にはわかりません。でも、そこには紀元前の数学者たちの鋭敏な数学的感覚が宿っているように感じるのです。 2000 年以上後になって「証明」された彼らの数学的感覚……そこには畏敬の念を抱かずにはいられません。